(本小题满分12分)
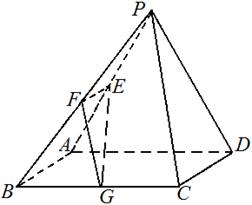
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(I)求证:EF 平面PAD;
平面PAD;
(II)求平面EFG与平面ABCD所成锐二面角的大小;
(III)若M为线段AB上靠近A的一个动点,问当AM长度等于多少时,直线MF与平面EFG所成角的正弦值等于 ?
?
推荐套卷
(本小题满分12分)
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(I)求证:EF 平面PAD;
平面PAD;
(II)求平面EFG与平面ABCD所成锐二面角的大小;
(III)若M为线段AB上靠近A的一个动点,问当AM长度等于多少时,直线MF与平面EFG所成角的正弦值等于 ?
?