一辆货车的最大载重量为
吨，要装载
、
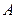两种不同的货物，已知装载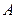货物每吨收入
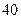元，装载货物每吨收入元，且要求装载的货物不少于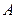货物的一半．请问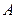、两种不同的货物分别装载多少吨时，载货得到的收入最大？并求出这个最大值．
相关试题
（本题满分12分)若函数
对任意的
，恒有
.当
时，恒有
.
（1）判断函数
的奇偶性，并证明你的结论；
（2）判断函数的单调性，并证明你的结论；
（3）若
，解不等式
.
是一次函数，且满足：
，求
，求
，
，若
，求实数
的取值范围.
（
，
，求函数
的最小值。
函数
．
的最小正周期。
的值。
，求
的值。推荐套卷
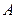一辆货车的最大载重量为吨，要装载、两种不同的货物，已知装载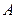货物每吨收入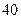元，装载货物每吨收入元，且要求装载的货物不少于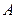货物的一半．请问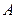、两种不同的货物分别装载多少吨时，载货得到的收入最大？并求出这个最大值．
（本题满分12分)若函数对任意的，恒有.当时，恒有.
（1）判断函数的奇偶性，并证明你的结论；
（2）判断函数的单调性，并证明你的结论；
（3）若，解不等式.
粤公网安备 44130202000953号