(本题14分)
某公司将进货单价为8元一个的商品按10元一个销售，每天可以卖出100个，若这种商品的销售价每个上涨一元，则销售量就减少8个．
（1）求销售价为13元时每天的销售利润；
（2）如果销售利润为336元，那么销售价上涨了几元？
（3）设销售价上涨x元（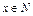
）试将利润y表示为x的函数，并求出上涨几元，可获最大利润．
相关试题
是正方形，
，
是
的中点．
；
，求三棱锥
的体积．
函数
。
的最小正周期和最大值．
的单调递增区间．
中,
分别是角
所对的边，且
．
的大小；
，且
，求
的值．
的前
项和为
，向量
,满足条件
．
，数列
满足条件
，
．
，求数列
的前
．
中,侧棱与底面垂直,
,
,点
为
的中点．
平面
;
上是否存在点
，使
平面
？若存在，试确定点
推荐套卷
(本题14分)
某公司将进货单价为8元一个的商品按10元一个销售，每天可以卖出100个，若这种商品的销售价每个上涨一元，则销售量就减少8个．
（1）求销售价为13元时每天的销售利润；
（2）如果销售利润为336元，那么销售价上涨了几元？
（3）设销售价上涨x元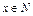（）试将利润y表示为x的函数，并求出上涨几元，可获最大利润．
粤公网安备 44130202000953号