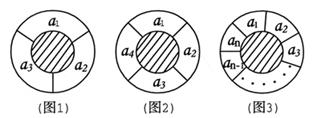
一个同心圆形花坛，分为两部分，中间小圆部分种植草坪和绿色灌木，周围的圆环分为n（n≥3，n∈N）等份，种植红、黄、蓝三色不同的花，要求相邻两部分种植不同颜色的花．
（1）如图1，圆环分成的3等份为a1，a2，a3，有多少不同的种植方法？如图2，圆环分成的4等份为a1，a2，a3，a4，有多少不同的种植方法？ 
（2）如图3，圆环分成的n等份为a1，a2，a3，……，an，有多少不同的种植方法？
相关试题
的不等式
.
.
时,求函数
的单调区间;
时
,求a的取值范围.
在点
处的切线方程;
的极值.
的极坐标方程是
，以极点为原点，极轴为
轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位.
作倾斜角为
的直线
与曲线
两点，求线段
的长度和
的值．推荐套卷
一个同心圆形花坛，分为两部分，中间小圆部分种植草坪和绿色灌木，周围的圆环分为n（n≥3，n∈N）等份，种植红、黄、蓝三色不同的花，要求相邻两部分种植不同颜色的花．
（1）如图1，圆环分成的3等份为a1，a2，a3，有多少不同的种植方法？如图2，圆环分成的4等份为a1，a2，a3，a4，有多少不同的种植方法？
（2）如图3，圆环分成的n等份为a1，a2，a3，……，an，有多少不同的种植方法？
粤公网安备 44130202000953号