注意:请考生在(1)、(2)、(3)三题中任选一题做答,如果多做,则按所做的第一题计分
(1)如图,AC为⊙O的直径,弦BD⊥AC于点P,PC=2,PA=8,
则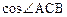 的值为 _____.
的值为 _____.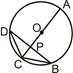
(2)在极坐标系中,圆 的圆心的极坐标是 _____.
的圆心的极坐标是 _____.
(3)不等式 的解集为 _____.
的解集为 _____.
相关知识点
推荐套卷
注意:请考生在(1)、(2)、(3)三题中任选一题做答,如果多做,则按所做的第一题计分
(1)如图,AC为⊙O的直径,弦BD⊥AC于点P,PC=2,PA=8,
则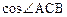 的值为 _____.
的值为 _____.
(2)在极坐标系中,圆 的圆心的极坐标是 _____.
的圆心的极坐标是 _____.
(3)不等式 的解集为 _____.
的解集为 _____.