（本小题满分12分）
甲乙两奥运会主办城市之间有7条网线并联，这7条网线能通过的信息量分别为1，1，2，2，2，3，3，现从中任选三条网线，设可通过的信息量为X，当可通过的信息最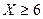
，则可保证信息通畅。
（I）求线路信息通畅的概率；
（II）求线路可通过的信息量X的分布列及数学期望。
相关试题
与直线
相切，且与定圆
外切，求动圆圆心
中，
，
，
，
，
，
是
的中点，设
，
，
．
表示
；
的长．
及点
．
在圆上，求线段
的长及直线
为圆
上任一点，求
的最大值和最小值；
满足
,求
的最大值和最小值．相关知识点
推荐套卷
（本小题满分12分）
甲乙两奥运会主办城市之间有7条网线并联，这7条网线能通过的信息量分别为1，1，2，2，2，3，3，现从中任选三条网线，设可通过的信息量为X，当可通过的信息最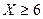，则可保证信息通畅。
（I）求线路信息通畅的概率；
（II）求线路可通过的信息量X的分布列及数学期望。
粤公网安备 44130202000953号