(本小题满分13分)
已知数列 满足:
满足: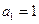 ,
,
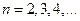
(I)求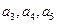 得值;
得值;
(II) 设 求证:数列
求证:数列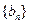 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(III) 对任意的 ,在数列
,在数列 中是否存在连续的
中是否存在连续的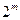 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这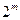 项,并证明这
项,并证明这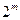 项构成等差数列;若不存在,说明理由。
项构成等差数列;若不存在,说明理由。
推荐套卷
(本小题满分13分)
已知数列 满足:
满足: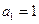 ,
,
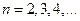
(I)求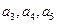 得值;
得值;
(II) 设 求证:数列
求证:数列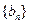 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(III) 对任意的 ,在数列
,在数列 中是否存在连续的
中是否存在连续的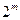 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这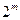 项,并证明这
项,并证明这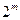 项构成等差数列;若不存在,说明理由。
项构成等差数列;若不存在,说明理由。