（满分13分）如图所示，将一个圆形的画板分成面积相等的三部分，
每部分上分别涂色为黄、红、蓝三色，某人随机向画板投射一只镖，
如果射中边界则重新再射，射中涂色部分则分别得分为3,2, 1分，
投射两次的得分为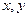
，记
．
求随机变量
的最大值，并求事件“取得最大值”的概率．
 |
与直线
的交点，且与点A（0，4）和点B（4，O）距离相等的直线方程.
是定义在
上的奇函数，且
，若
时，有
成立.
；
时，
对所有的
恒成立，求实数
的取值范围.
，若
在
上的最大值为
，求
，集合
.
，求
的值；（2）若
，求
，判断
在
上的单调性，并证明.相关知识点
推荐套卷
（满分13分）如图所示，将一个圆形的画板分成面积相等的三部分，
每部分上分别涂色为黄、红、蓝三色，某人随机向画板投射一只镖，
如果射中边界则重新再射，射中涂色部分则分别得分为3,2, 1分，
投射两次的得分为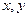，记．
求随机变量的最大值，并求事件“取得最大值”的概率．
|
粤公网安备 44130202000953号