某突发事件,在不采取任何预防措施的情况下发生的概率为 ,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为
,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为 和
和 .若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
(注:总费用 = 采取预防措施的费用+发生突发事件损失的期望值)
相关知识点
推荐套卷
 ,答对文科题的概率均为
,答对文科题的概率均为 ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分 的分布列与数学期望
的分布列与数学期望 .
.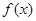 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的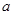 、
、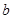 ∈R,都满足
∈R,都满足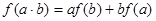 ,若
,若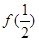 =1,
=1, .
.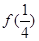 、
、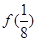 、
、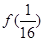 的值;
的值;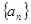 通项公式,并用数学归纳法证明.
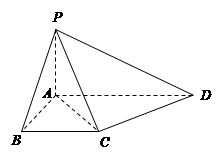
通项公式,并用数学归纳法证明.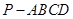 中,底面
中,底面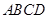 为直角梯形,且
为直角梯形,且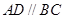 ,
, ,侧面
,侧面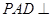 底面
底面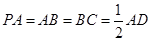 .
.
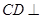 平面
平面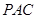 ;
;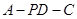 的余弦值.
的余弦值. (
(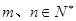 )的展开式中
)的展开式中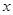 的系数为11.
的系数为11.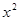 的系数的最小值;
的系数的最小值;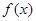 展开式中
展开式中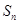 ,且满足
,且满足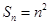 ,数列
,数列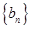 满足
满足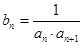 ,
,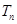 为数列
为数列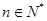 ,不等式
,不等式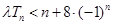 恒成立,求实数
恒成立,求实数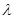 的取值范围;
的取值范围;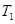 ,
,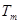 ,
, 粤公网安备 44130202000953号
粤公网安备 44130202000953号