某突发事件,在不采取任何预防措施的情况下发生的概率为 ,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为
,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为 和
和 .若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
(注:总费用 = 采取预防措施的费用+发生突发事件损失的期望值)
相关知识点
推荐套卷
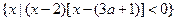 ,
,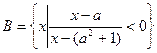 .
.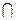 B;(Ⅱ)求使B
B;(Ⅱ)求使B A的实数a的取值范围.
A的实数a的取值范围.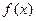 是定义域为[-3,3]的函数,并且设
是定义域为[-3,3]的函数,并且设 ,
, ,其中常数c为实数.(1)求
,其中常数c为实数.(1)求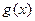 和
和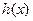 的定义域;(2)如果
的定义域;(2)如果 的自变量
的自变量 的取值范围.
的取值范围. 为奇函数,导函数
为奇函数,导函数 的最小值为-12,函数
的最小值为-12,函数 的图象在点P
的图象在点P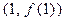 处的切线与直线
处的切线与直线 垂直.(1)求a,b,c的值;(2)求
垂直.(1)求a,b,c的值;(2)求 的各个单调区间,并求
的各个单调区间,并求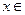 [-1, 3]时的最大值和最小值.
[-1, 3]时的最大值和最小值.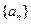 中,
中,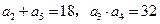 ,并且
,并且 (1)求
(1)求 以及数列
以及数列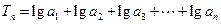 ,求当
,求当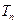 最大时
最大时 的值.
的值. ,其中向量
,其中向量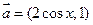 ,
, (1)求函数
(1)求函数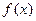 的最小正周期和单调递增区间;(2)当
的最小正周期和单调递增区间;(2)当 时,求函数
时,求函数 粤公网安备 44130202000953号
粤公网安备 44130202000953号