在区间
上，如果函数
为增函数，而函数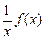
为减函数，则称函数为“弱增”函数．已知函数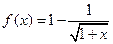
（1）判断函数在区间
上是否为“弱增”函数
（2）设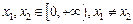
，证明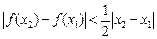
（3）当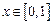
时，不等式
恒成立，求实数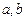
的取值范围
．
的最小正周期和单调增区间．
的图象经过怎样的变换得到？
，求
的值．
为第四象限角，其终边上的一个点是
，且
，求
和
．
中，
是数列
项和，对任意
，有 
．
，求数列
的前
．
中，
为常数，
，且
成公比不等于1的等比数列．
的值；
，求数列
的前
项和
相关知识点
推荐套卷
在区间上，如果函数为增函数，而函数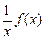为减函数，则称函数为“弱增”函数．已知函数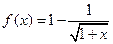
（1）判断函数在区间上是否为“弱增”函数
（2）设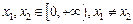，证明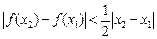
（3）当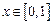时，不等式恒成立，求实数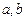的取值范围
粤公网安备 44130202000953号