(本小题满分12分)甲、乙两所学校的代表队参加汉字听写大赛.在比赛第二阶段,两队各剩最后两名队员上场.甲队两名队员通过第二阶段比赛的概率分别是 和
和 ,乙队两名队员通过第二阶段比赛的概率都是
,乙队两名队员通过第二阶段比赛的概率都是 .通过了第二阶段比赛的队员,才能进入第三阶段比赛(若某队两个队员都没有通过第二阶段的比赛,则该队进入第三阶段比赛人数为
.通过了第二阶段比赛的队员,才能进入第三阶段比赛(若某队两个队员都没有通过第二阶段的比赛,则该队进入第三阶段比赛人数为 ).所有参赛队员比赛互不影响,其过程、结果都是彼此独立的.
).所有参赛队员比赛互不影响,其过程、结果都是彼此独立的.
(Ⅰ)求第三阶段比赛,甲、乙两队人数相等的概率;
(Ⅱ) 表示第三阶段比赛甲、乙两队的人数差的绝对值,求
表示第三阶段比赛甲、乙两队的人数差的绝对值,求 的分布列和数学期望.
的分布列和数学期望.
相关知识点
推荐套卷
 .
.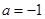 时,解不等式
时,解不等式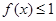 ;
; 时,
时, ,求
,求 的取值范围.
的取值范围. 的参数方程为
的参数方程为 为参数,
为参数, ),直线
),直线 在参数方程是
在参数方程是 为参数),曲线
为参数),曲线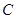 与直线
与直线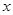 轴上,以坐标原点为极点,
轴上,以坐标原点为极点,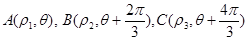 在曲线
在曲线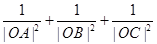 的值。
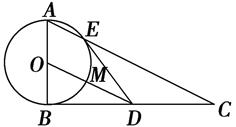
的值。 是直角三角形,
是直角三角形,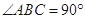 .以
.以 为直径的圆
为直径的圆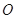 交
交 于点
于点 ,点
,点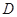 是
是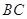 边的中点.连结
边的中点.连结 交圆
交圆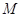 .
.
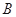 、
、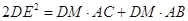
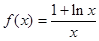 .
.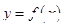 的单调区间;
的单调区间; 的方程
的方程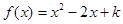 有实数解,求实数
有实数解,求实数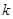 的取值范围;
的取值范围;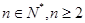 时,求证:
时,求证: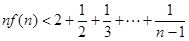
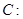

 是抛物线
是抛物线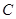 上一点,求证过点
上一点,求证过点 的抛物线
的抛物线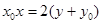 ;
;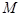 是抛物线
是抛物线 ,求
,求 的最小值,并求相应的点
的最小值,并求相应的点 粤公网安备 44130202000953号
粤公网安备 44130202000953号