(本小题满分12分)某军区新兵 步枪射击个人平均成绩
步枪射击个人平均成绩 (单位:环)服从正态分布
(单位:环)服从正态分布 ,从这些个人平均成绩中随机抽取
,从这些个人平均成绩中随机抽取 个,得到如下频数分布表:
个,得到如下频数分布表:
 |
 |
 |
 |
 |
 |
 |
| 频数 |
 |
 |
 |
 |
 |
 |
(Ⅰ)求 和
和 的值(用样本数学期望、方差代替总体数学期望、方差);
的值(用样本数学期望、方差代替总体数学期望、方差);
(Ⅱ)如果这个军区有新兵 名,试估计这个军区新兵
名,试估计这个军区新兵 步枪射击个人平均成绩在区间
步枪射击个人平均成绩在区间 上的人数
上的人数
[参考数据: ,若
,若 ,则
,则 ,
, ,
, ].
].
相关知识点
推荐套卷
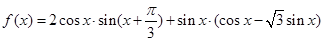
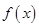 的最小正周期和单调递减区间;
的最小正周期和单调递减区间; 中,
中,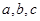 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若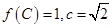 ,求
,求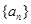 的前
的前 项和为
项和为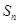 ,且
,且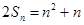 2.
2.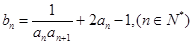 求数列
求数列
 的前
的前 项和
项和 ,
, 粤公网安备 44130202000953号
粤公网安备 44130202000953号