(本小题满分10分)
某校有学生会干部7名，其中男干部有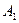
，A
，A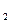
，A
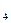共4人；女干部有B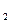
，B，B共3人．从中选出男、女干部各1名，组成一个小组参加某项活动．
（Ⅰ）求A被选中的概率；
（Ⅱ）求A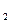，B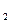 不全被选中的概率．
相关试题
中，
所对的边分别是
，不等式
对一切实数
恒成立．
的取值范围；
取最大值，且
时，求
的前n项和为
，且
，数列
为等差数列，且
．
，求数列
的前n项和
．
中，若
．
的大小；
求
的值
，
的解集
．求
的值；
求
的最小值．
，函数
．
的单调区间和值域；
，若
，总
，使得
成立，求
的取值范围；
，证明：
．推荐套卷
(本小题满分10分)
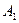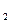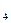某校有学生会干部7名，其中男干部有，A，A，A共4人；女干部有B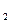，B，B共3人．从中选出男、女干部各1名，组成一个小组参加某项活动．
（Ⅰ）求A被选中的概率；
（Ⅱ）求A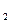，B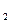 不全被选中的概率．
粤公网安备 44130202000953号