.(本小题满分14分)
已知等比数列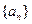 的前
的前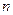 项和
项和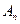 =
=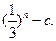 数列
数列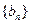
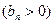 的首项为
的首项为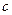 ,且前
,且前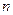 项和
项和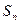 满足
满足 -
-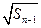 =1(
=1(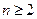 .)
.)
(1)求数列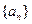 的通项公式
的通项公式
(2)求数列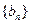 的通项公式
的通项公式
(3)若数列{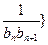 前
前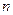 项和为
项和为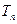 ,问
,问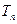 >
>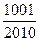 的最小正整数
的最小正整数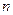 是多少?
是多少?
推荐套卷
.(本小题满分14分)
已知等比数列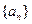 的前
的前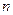 项和
项和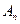 =
=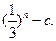 数列
数列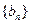
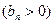 的首项为
的首项为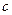 ,且前
,且前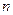 项和
项和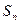 满足
满足 -
-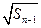 =1(
=1(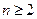 .)
.)
(1)求数列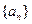 的通项公式
的通项公式
(2)求数列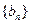 的通项公式
的通项公式
(3)若数列{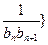 前
前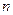 项和为
项和为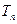 ,问
,问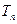 >
>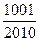 的最小正整数
的最小正整数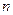 是多少?
是多少?