(本小题满分14分)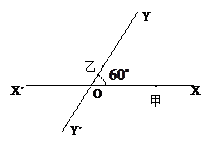
如图,有两条相交成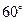 的直路
的直路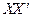 ,
,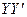 ,交点是
,交点是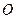 ,甲、乙分别在
,甲、乙分别在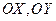 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿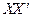 方向用2 km/h的速度,乙沿
方向用2 km/h的速度,乙沿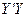 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在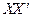 上点A处,乙在
上点A处,乙在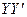 上点B处.
上点B处.
(Ⅰ)求t=1.5时,甲、乙两人之间的距离;
(Ⅱ)求t=2时,甲、乙两人之间的距离;
(Ⅲ) 当t为何值时,甲、乙两人之间的距离最短?
推荐套卷
(本小题满分14分)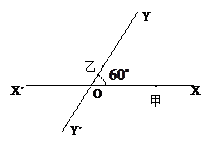
如图,有两条相交成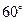 的直路
的直路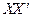 ,
,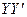 ,交点是
,交点是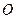 ,甲、乙分别在
,甲、乙分别在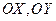 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿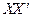 方向用2 km/h的速度,乙沿
方向用2 km/h的速度,乙沿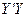 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在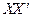 上点A处,乙在
上点A处,乙在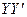 上点B处.
上点B处.
(Ⅰ)求t=1.5时,甲、乙两人之间的距离;
(Ⅱ)求t=2时,甲、乙两人之间的距离;
(Ⅲ) 当t为何值时,甲、乙两人之间的距离最短?