如图:某污水处理厂要在一个矩形  污水处理池
污水处理池 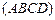 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 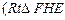 ,
, 
 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口  是
是 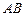 的中
的中  点,
点,  分
分  别落在线段
别落在线段 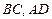 上.已知
上.已知  米,
米, 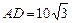 米,记
米,记  .
.

(Ⅰ)试将污水净化管道的长度  表示为
表示为  的函数
的函数
并写出定义域
(Ⅱ)若 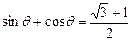 ,求此时管道的长度
,求此时管道的长度 
(Ⅲ)问:当  取何值时,铺设管道的
取何值时,铺设管道的  成本最低?并
成本最低?并  求出此时管道的长度
求出此时管道的长度
推荐套卷
如图:某污水处理厂要在一个矩形  污水处理池
污水处理池 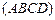 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 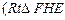 ,
, 
 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口  是
是 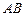 的中
的中  点,
点,  分
分  别落在线段
别落在线段 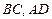 上.已知
上.已知  米,
米, 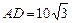 米,记
米,记  .
.

(Ⅰ)试将污水净化管道的长度  表示为
表示为  的函数
的函数
并写出定义域
(Ⅱ)若 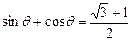 ,求此时管道的长度
,求此时管道的长度 
(Ⅲ)问:当  取何值时,铺设管道的
取何值时,铺设管道的  成本最低?并
成本最低?并  求出此时管道的长度
求出此时管道的长度