某地预计从年初开始的前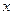
个月内，对某种商品的需求总量
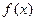（万件）与月份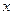的近似关系为
。
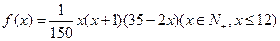①写出今年第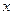个月的需求量
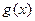（万件）与月份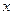的函数关系，并求出哪些个月份的需求量超过1.4万件；
②如果将该商品每月初都投放市场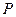
万件，要保证每个月都能满足供应，则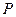至少为多少万件？
相关试题
的图象过点
．
的值；
中，若
，求
的取值范围．
中，
，
，求角
的大小．
、
、
是同一平面内的三个向量，其中
．
，且
，求
，且
与
垂直，求
．
中，设
，
，又
，
，向量
，
的夹角为．
表示
；
是
边的中点，直线
交
于
点，求
．
的顶点在原点，始边与
轴的正半轴重合，终边经过点
．
的值；
，求函数
在区间
上的值域．推荐套卷
某地预计从年初开始的前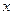个月内，对某种商品的需求总量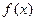（万件）与月份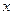的近似关系为。
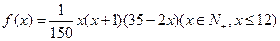①写出今年第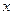个月的需求量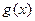（万件）与月份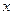的函数关系，并求出哪些个月份的需求量超过1.4万件；
②如果将该商品每月初都投放市场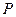万件，要保证每个月都能满足供应，则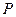至少为多少万件？
粤公网安备 44130202000953号