(本小题满分15分)
如图,某市拟在道路AE的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数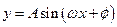 (
(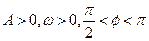 ),
),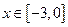 的图象,且图象的最高点为
的图象,且图象的最高点为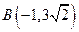 ;赛道的中间部分为
;赛道的中间部分为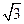 千米的水平跑道
千米的水平跑道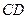 ;赛道的后一部分为以O为圆心的一段圆弧
;赛道的后一部分为以O为圆心的一段圆弧 .
.
(1)求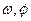 的值和角
的值和角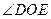 的值;
的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时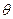 的值.
的值.
推荐套卷
(本小题满分15分)
如图,某市拟在道路AE的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数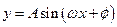 (
(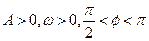 ),
),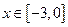 的图象,且图象的最高点为
的图象,且图象的最高点为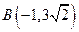 ;赛道的中间部分为
;赛道的中间部分为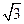 千米的水平跑道
千米的水平跑道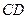 ;赛道的后一部分为以O为圆心的一段圆弧
;赛道的后一部分为以O为圆心的一段圆弧 .
.
(1)求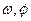 的值和角
的值和角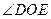 的值;
的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时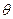 的值.
的值.