（满分12分）
某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算，如果将楼房建为x（x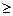
10）层，则每平方米的平均建筑费用为560+48x（单位：元）。为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=
）
为
所在平面外一点，
，
，且
，求证：
面
。
交正方形
于
，
、
在对角线
、
上，且
，求证：
平面
。
、
异面，求证过
α ,m
α ,l∥m推荐套卷
（满分12分）
某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算，如果将楼房建为x（x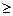10）层，则每平方米的平均建筑费用为560+48x（单位：元）。为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=）
粤公网安备 44130202000953号