(本小题10分)
如图,已知AP是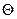 O的切线,P为切点,AC是
O的切线,P为切点,AC是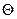 O的割线,与
O的割线,与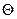 O交于B,C两点,圆心O在
O交于B,C两点,圆心O在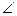 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。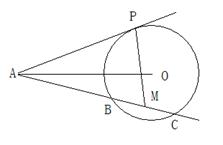
(1) 证明:A,P,O,M四点共圆;
(2) 求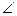 OAM+
OAM+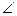 APM的大小。
APM的大小。
相关知识点
推荐套卷
(本小题10分)
如图,已知AP是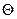 O的切线,P为切点,AC是
O的切线,P为切点,AC是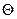 O的割线,与
O的割线,与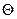 O交于B,C两点,圆心O在
O交于B,C两点,圆心O在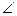 PAC的内部,点M是BC的中点。
PAC的内部,点M是BC的中点。
(1) 证明:A,P,O,M四点共圆;
(2) 求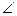 OAM+
OAM+ APM的大小。
APM的大小。