空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.1月某日某省x个监测点数据统计如下:

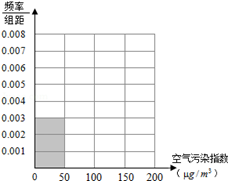
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)若A市共有5个监测点,其中有3个监测点为轻度污染,2个监测点为良.从中任意选取2个监测点,事件A“其中至少有一个为良”发生的概率是多少?