已知动圆M过定点P（0，m）(m>0)，且与定直线
相切，动圆圆心M的轨迹方程为C，直线
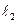过点P 交曲线C于A、B两点。
(1)若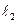交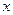
轴于点S,求
的取值范围；
（2）若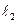的倾斜角为
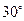，在
上是否存在点E使△ABE为正三角形? 若能，求点E的坐标；若不能，说明理由.
，其中
为正实数
时，求
的极值点；
上的单调函数，求
的图象与
在原点相切，且函数的极小值为
，（1）求
的值；（2）求函数的递减区间．
：函数
在
上递增；命题
：函数
的定义域为R．若
的取值范围．
的三个顶点为
，求：
有最大值
，试求实数
的值.相关知识点
推荐套卷
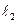已知动圆M过定点P（0，m）(m>0)，且与定直线相切，动圆圆心M的轨迹方程为C，直线过点P 交曲线C于A、B两点。
(1)若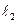交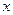轴于点S,求的取值范围；
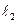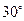（2）若的倾斜角为，在上是否存在点E使△ABE为正三角形? 若能，求点E的坐标；若不能，说明理由.
粤公网安备 44130202000953号