某中学举行了一次“上海世博会知识竞赛”,从全校参加竞赛的学生的试卷中,随机抽取了一个样本,考察竞赛的成绩分布(得分均为整数,满分100分),将样本分成5组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为1:3:6:4:2,最右边一组的频数是6.请结合直方图提供的信息,解答下列问题:
(Ⅰ)样本容量是多少?(Ⅱ)成绩落在那个范围内的人数最多?并求该小组的频数、频率;(Ⅲ)估计这次竞赛中,成绩高于60分的学生占总人数的百分比.
相关知识点
推荐套卷
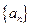 中,
中,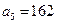 ,公比
,公比 ,前
,前 项和
项和 ,求首项
,求首项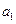 和项数
和项数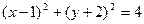 ,求
,求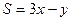 的最值
的最值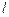 经过点P(1,1),
经过点P(1,1),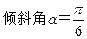 。
。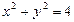 相交于两点A、B,求点P到A,B两点的距离之积
相交于两点A、B,求点P到A,B两点的距离之积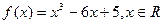 .
.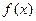 的单调区间和极值;
的单调区间和极值;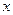 的方程
的方程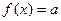 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.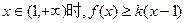 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.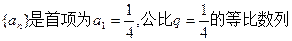 ,设
,设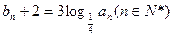 ,数列
,数列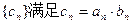 。
。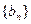 是等差数列;
是等差数列;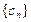 的前n项和
的前n项和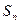 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号