(本小题满分14分).如图所示,平面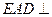 平面
平面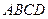 ,
,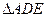 是等边三角形,
是等边三角形,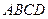 是矩形,
是矩形,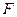 是
是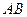 的中点,
的中点,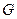 是
是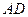 的中点,
的中点,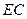 与平面
与平面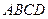 成
成 角
角


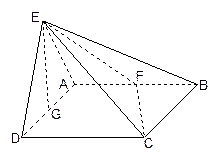
(1)求证: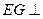 平面
平面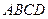 ;
;
(2)若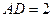 ,求二面角
,求二面角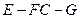 的度数;
的度数;
(3)当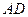 的长是多少时,
的长是多少时,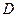 点到平面
点到平面 的距离为
的距离为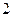 ?并说明理由
?并说明理由
推荐套卷
(本小题满分14分).如图所示,平面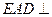 平面
平面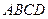 ,
,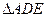 是等边三角形,
是等边三角形,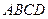 是矩形,
是矩形,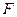 是
是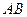 的中点,
的中点,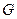 是
是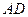 的中点,
的中点,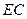 与平面
与平面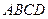 成
成 角
角


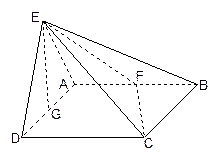
(1)求证: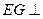 平面
平面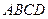 ;
;
(2)若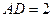 ,求二面角
,求二面角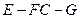 的度数;
的度数;
(3)当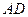 的长是多少时,
的长是多少时,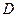 点到平面
点到平面 的距离为
的距离为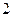 ?并说明理由
?并说明理由