(本小题13分) 如图所示, PQ为平面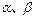
的交线, 已知二面角
为直二面角, 
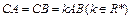, ∠BAP＝45°. 
（1）证明: BC⊥PQ;
（2）设点C在平面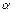
内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心？
（3）当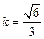
时, 求二面角B－AC－P的大小.
相关试题
(i为虚数单位)
是实数，且－1＜ω＜2
，求证：u为纯虚数；
，是否存在整式
，使得
对n≥2的一切自然数都成立?并试用数学
的展开式中，第6项与第7的系数相等,求展开式中二项式系数最大的项和系数最大的项．
求证:
推荐套卷
(本小题13分) 如图所示, PQ为平面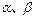的交线, 已知二面角为直二面角, 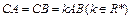, ∠BAP＝45°.
（1）证明: BC⊥PQ;
（2）设点C在平面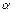内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心？
（3）当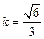时, 求二面角B－AC－P的大小.
粤公网安备 44130202000953号