(本小题12分) 如图,四棱锥P-ABCD的底面是正方形, PA⊥底面ABCD, PA=2,
∠PDA="45°," 点E、F分别为棱AB、PD的中点. 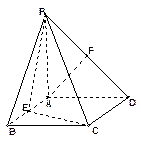
(1)求证: AF∥平面PCE;
(2)求证: 平面PCE⊥平面PCD;
(3)求AF与平面PCB所成的角的大小.
推荐套卷
(本小题12分) 如图,四棱锥P-ABCD的底面是正方形, PA⊥底面ABCD, PA=2,
∠PDA="45°," 点E、F分别为棱AB、PD的中点. 
(1)求证: AF∥平面PCE;
(2)求证: 平面PCE⊥平面PCD;
(3)求AF与平面PCB所成的角的大小.