(本小题满分15分)
已知曲线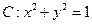 ,若按向量
,若按向量 作平移变换得曲线
作平移变换得曲线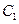 ;若将曲线
;若将曲线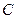 按伸缩系数
按伸缩系数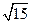 向着
向着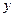 轴作伸缩变换,再按伸缩系数3向着
轴作伸缩变换,再按伸缩系数3向着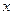 轴作伸缩变换得到曲线
轴作伸缩变换得到曲线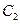
(1)求曲线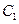 及
及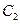 方程;
方程;
(2)若 为
为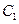 上一点,
上一点, 为
为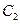 上任意一点,且
上任意一点,且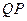 与曲线
与曲线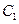 相切(
相切( 为切点),
为切点),
求线段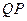 的最大值及对应的
的最大值及对应的 点坐标.
点坐标.
推荐套卷
(本小题满分15分)
已知曲线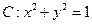 ,若按向量
,若按向量 作平移变换得曲线
作平移变换得曲线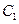 ;若将曲线
;若将曲线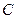 按伸缩系数
按伸缩系数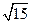 向着
向着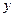 轴作伸缩变换,再按伸缩系数3向着
轴作伸缩变换,再按伸缩系数3向着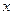 轴作伸缩变换得到曲线
轴作伸缩变换得到曲线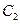
(1)求曲线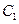 及
及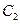 方程;
方程;
(2)若 为
为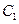 上一点,
上一点, 为
为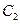 上任意一点,且
上任意一点,且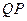 与曲线
与曲线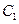 相切(
相切( 为切点),
为切点),
求线段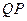 的最大值及对应的
的最大值及对应的 点坐标.
点坐标.