(本题16分)函数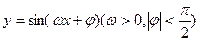 在同一个周期内,当
在同一个周期内,当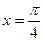 时
时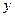 取最大值1,当
取最大值1,当 时,
时,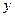 取最小值
取最小值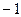 。
。
(1)求函数的解析式
(2)函数 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到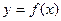 的图象?
的图象?
(3)若函数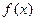 满足方程
满足方程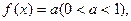 求在
求在 内的所有实数根之和.
内的所有实数根之和.
相关知识点
推荐套卷
(本题16分)函数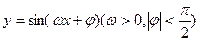 在同一个周期内,当
在同一个周期内,当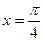 时
时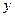 取最大值1,当
取最大值1,当 时,
时,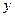 取最小值
取最小值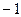 。
。
(1)求函数的解析式
(2)函数 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到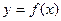 的图象?
的图象?
(3)若函数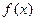 满足方程
满足方程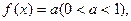 求在
求在 内的所有实数根之和.
内的所有实数根之和.