已知点集L={(x,y)|y=m·n},其中m=(2x-2b,1),n=(1,1+2b),点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)求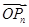 ·OPn+1的最小值;
·OPn+1的最小值;
(3)设cn=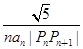 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.
相关知识点
推荐套卷
已知点集L={(x,y)|y=m·n},其中m=(2x-2b,1),n=(1,1+2b),点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)求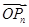 ·OPn+1的最小值;
·OPn+1的最小值;
(3)设cn=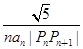 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.