（本小题满分14分）一束光线
通过点M（-3，3）射到x轴上，然后反射到圆C上，其中圆C满足以下条件：过点A（1，2）和点B（2，3）且圆心在直线
上。
（1）求圆C的方程；
（2）求通过圆C圆心的反射光线所在直线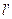
的方程；
（3）若反射光线所在直线与圆C相切，求入射光线所在直线的方程
相关试题
中，
、
、
分别是三内角
、
、
的对边，已知
．
，判断
的定义域为
，
时，求
的最小值．
，
．命题
，命题
，且命题
是命题
的充分条件，求实数
的取值范围．
，若
在点
处的切线斜率为
．
表示
；
，若
对定义域内的
恒成立，
，证明：
．
：
的左焦点为
，右焦点为
．
过点
垂直
的垂直平分线交
的方程；
为坐标原点，取曲线
，以
为直径作圆与
，求该圆的面积最小时点相关知识点
推荐套卷
（本小题满分14分）一束光线通过点M（-3，3）射到x轴上，然后反射到圆C上，其中圆C满足以下条件：过点A（1，2）和点B（2，3）且圆心在直线上。
（1）求圆C的方程；
（2）求通过圆C圆心的反射光线所在直线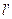的方程；
（3）若反射光线所在直线与圆C相切，求入射光线所在直线的方程
粤公网安备 44130202000953号