（本小题满分12分）
将如下6个函数：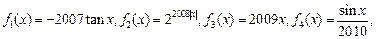
，分别写在6张小卡片上，放入盒中.
（Ⅰ）现从盒子中任取2张卡片，将卡片上的函数相加得到一个新函数，求所得函数是偶函数的概率；
（Ⅱ）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有奇函数卡片则停止抽取，否则继续进行，求抽取次数
的分布列和数学期望.
的模为
，求
的最大值．
，
，求满足
的复数
．
，点
对应的复数
，
对应的复数为
，向量
对应的复数为
，求点
对应的复数．
为虚数，求证：
为纯虚数的充要条件是：
．
满足
，
的虚部是2．
在复平面上的对应点分别为
，求
的面积．推荐套卷
（本小题满分12分）
将如下6个函数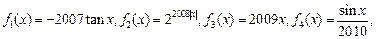：，分别写在6张小卡片上，放入盒中.
（Ⅰ）现从盒子中任取2张卡片，将卡片上的函数相加得到一个新函数，求所得函数是偶函数的概率；
（Ⅱ）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有奇函数卡片则停止抽取，否则继续进行，求抽取次数的分布列和数学期望.
粤公网安备 44130202000953号