已知抛物线
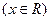与坐标轴有三个交点，经过这三点的圆记为
.
（1）求实数
的取值范围；
（2）设抛物线与ｘ轴的交点从左到右分别为A、B，与ｙ轴的交点为C，求A、B、C三点的坐标；
（3）设直线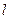
是抛物线在点A处的切线，试判断直线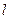是否也是圆的切线？并说明理由.
的值；
（其中
，且a为常数）时，f（x）是否存在最小值，如果存在，求出最小值；如果不存在，请说明理由。
。
为实数，函数
，
． 
的奇偶性； （2）求 
是定义在
上的奇函数，当
时，
，
.
在
上是增函数.推荐套卷
已知抛物线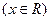与坐标轴有三个交点，经过这三点的圆记为.
（1）求实数的取值范围；（2）设抛物线与ｘ轴的交点从左到右分别为A、B，与ｙ轴的交点为C，求A、B、C三点的坐标；
（3）设直线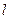是抛物线在点A处的切线，试判断直线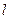是否也是圆的切线？并说明理由.
粤公网安备 44130202000953号