对于数列
，定义“
变换”：将数列
变换成数列
，其中
，且
，这种“变换”记作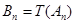
.继续对数列
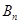进行“变换”，得到数列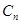
，…，依此类推，当得到的数列各项均为
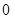时变换结束．
（Ⅰ）试问
和
经过不断的“变换”能否结束？若能，请依次写出经过“变换”得到的各数列；若不能，说明理由；
（Ⅱ）求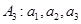
经过有限次“变换”后能够结束的充要条件；
（Ⅲ）证明：
一定能经过有限次“变换”后结束．
，
两点，且截
轴所得的弦长为
．求此圆的方程．
，
两点，且在两坐标轴上的四个截距之和为
的圆的方程．
和
轴相切，圆心在直线
上，且被直线
截得的弦长为
，求圆
，
轴上分别截得弦长为
和
，且圆心在直线
上，求此圆方程．
的顶点
，
的坐标分别是
，
，顶点
在圆
上运动，求
的轨迹方程．推荐套卷
对于数列，定义“变换”：将数列变换成数列，其中，且，这种“变换”记作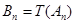.继续对数列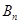进行“变换”，得到数列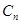，…，依此类推，当得到的数列各项均为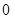时变换结束．
（Ⅰ）试问和经过不断的“变换”能否结束？若能，请依次写出经过“变换”得到的各数列；若不能，说明理由；
（Ⅱ）求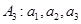经过有限次“变换”后能够结束的充要条件；
（Ⅲ）证明：一定能经过有限次“变换”后结束．
粤公网安备 44130202000953号