如图,在长方体
中,
分别是棱
上的点(点
与
不重合),且
. 过
的平面与棱
相交,交点分别为
.
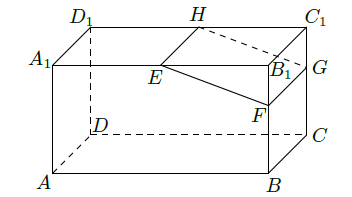
(I)证明: 平面 ;
(II)设 .在长方体 内随机选取一点.记该点取自几何体 内的概率为 ,当点 分别在棱 上运动且满足 时,求 的最小值.
推荐套卷
如图,在长方体
中,
分别是棱
上的点(点
与
不重合),且
. 过
的平面与棱
相交,交点分别为
.

(I)证明: 平面 ;
(II)设 .在长方体 内随机选取一点.记该点取自几何体 内的概率为 ,当点 分别在棱 上运动且满足 时,求 的最小值.