（本小题满分12分）要建造一个容积为2000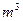
，深为5
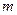的长方体无盖蓄水池，池壁的造价为95
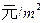，池底的造价为135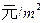，若水池底的一边长为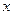
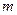，水池的总造价为
元。（1）把水池总造价
表示为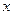的函数。（2）当水池
的长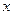为多少时，水池的总造价最少？
相关试题
的图象经过点
，且在
处的切线方程是
的解析式；（2）求
与
在
处的切线互相垂直，求
的值 
与直线
相交于两点
，且
为原点）.
为定值；（2）若离心率
，求椭圆长轴的取值范围。
轴为对称轴，焦点在直线
上．
是抛物线上一点，点
的坐标为
，求
的最小值（用
表示），并指出此时点推荐套卷
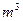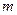（本小题满分12分）要建造一个容积为2000，深为5的长方体无盖蓄水池，池壁的造价为95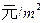，池底的造价为135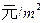，若水池底的一边长为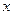 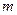，水池的总造价为元。（1）把水池总造价表示为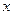的函数。（2）当水池的长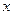为多少时，水池的总造价最少？
粤公网安备 44130202000953号