如图的多面体是底面为平行四边形的直四棱柱ABCD—
，经平面AEFG
所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60
(I)求证：BD⊥平面ADG；(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值．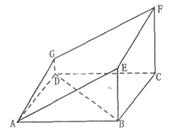
推荐套卷
如图的多面体是底面为平行四边形的直四棱柱ABCD—，经平面AEFG
所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60
(I)求证：BD⊥平面ADG；(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值．
粤公网安备 44130202000953号