如图,FD垂直于矩形ABCD所在平面,CE//DF, ∠DEF=900。
(1)求证:BE//平面ADF; (2)若矩形ABCD的一个边AB="3," 另一边BC=2
(2)若矩形ABCD的一个边AB="3," 另一边BC=2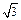 ,EF=2
,EF=2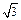 ,求几何体ABCDEF的体积。
,求几何体ABCDEF的体积。
相关知识点
推荐套卷
如图,FD垂直于矩形ABCD所在平面,CE//DF, ∠DEF=900。
(1)求证:BE//平面ADF; (2)若矩形ABCD的一个边AB="3," 另一边BC=2
(2)若矩形ABCD的一个边AB="3," 另一边BC=2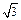 ,EF=2
,EF=2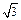 ,求几何体ABCDEF的体积。
,求几何体ABCDEF的体积。