 如图,已知椭圆
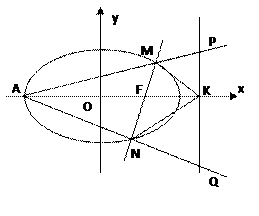
如图,已知椭圆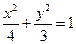 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.
(Ⅰ)求证:KF平分∠MKN;
(Ⅱ)直线AM、AN分别交准线 于点P、Q,
于点P、Q,
设直线MN的倾斜角为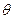 ,试用
,试用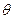 表示
表示
线段PQ的长度|PQ|,并求|PQ|的最小值.
推荐套卷
 如图,已知椭圆
如图,已知椭圆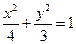 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.
(Ⅰ)求证:KF平分∠MKN;
(Ⅱ)直线AM、AN分别交准线 于点P、Q,
于点P、Q,
设直线MN的倾斜角为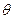 ,试用
,试用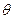 表示
表示
线段PQ的长度|PQ|,并求|PQ|的最小值.