(本小题满分14分)
如图,在棱长为a的正方体ABCD—A1B1C1D1中,E、F分别为棱AB和BC的中点,EF交BD于H。
(1)求二面角B1—EF—B的正切值;
(2)试在棱B1B上找一点M,使D1M⊥平面EFB1,并证明你的结论;
(3)求点D1到平面EFB1的距离。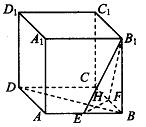
推荐套卷
(本小题满分14分)
如图,在棱长为a的正方体ABCD—A1B1C1D1中,E、F分别为棱AB和BC的中点,EF交BD于H。
(1)求二面角B1—EF—B的正切值;
(2)试在棱B1B上找一点M,使D1M⊥平面EFB1,并证明你的结论;
(3)求点D1到平面EFB1的距离。