双曲线M的中心在原点，并以椭圆
的焦点为焦点，以抛物线
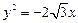的准线为右准线.
（1）求双曲线M的方程；
（2）设直线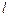
：
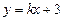与双曲线M相交于A、B两点，O是原点.
① 当
为何值时，使得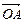
?
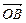
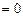② 是否存在这样的实数,使A、B两点关于直线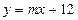
对称？若存在，求出的值；若不存在，说明理由.
：
和
：
，
，求
的值；
，试确定
|≤2,q:x2－2x+1－m2≤0(m>0),若
是
的必要而不充分条件， 求实数m的取值范围.
推荐套卷
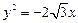双曲线M的中心在原点，并以椭圆的焦点为焦点，以抛物线的准线为右准线.
（1）求双曲线M的方程；
（2）设直线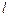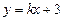：与双曲线M相交于A、B两点，O是原点.
① 当为何值时，使得?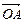
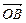
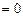② 是否存在这样的实数,使A、B两点关于直线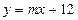对称？若存在，求出的值；若不存在，说明理由.
粤公网安备 44130202000953号