（本小题满分12分）如图，在长方体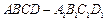
中，已知底面ABCD是边长为1的正方形，侧棱
，P是侧棱
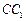上的一点，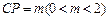
.
（Ⅰ）试问直线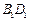
与AP能否垂直？并说明理由；
（Ⅱ）试确定m，使直线AP与平面BDD1B1所成角为60º；（Ⅲ）若m=1，求平面PA1D1与平面PAB所成角的大小.
的最小值.
，且与直线2x-y+4=0的交点在x轴上的直线的方程。
的直线的方程.推荐套卷
（本小题满分12分）如图，在长方体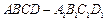
中，已知底面ABCD是边长为1的正方形，侧棱
，P是侧棱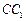上的一点，.
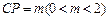（Ⅰ）试问直线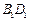与AP能否垂直？并说明理由；
（Ⅱ）试确定m，使直线AP与平面BDD1B1所成角为60º；（Ⅲ）若m=1，求平面PA1D1与平面PAB所成角的大小.
粤公网安备 44130202000953号