（本小题满分14分）已知四棱锥P—ABCD的三视图如右图所示，
其中正（主）视图与侧（左）视为直角三角形，俯视图为正方形。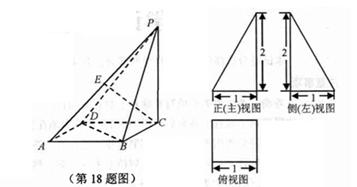
（1）求四棱锥P—ABCD的体积；
（2）若E是侧棱
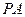上的动点。问：不论点E在PA的
任何位置上，是否都有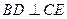
？
请证明你的结论？
（3）求二面角D—PA—B的余弦值。
相关试题
为偶函数．
的值；
，
，判断
与
的关系；
时，若函数
的值域为
，求
的值.
是定义在
上的减函数，满足
.
；
，解不等式
.
.
在
上为减函数.
上的最小值.
的两个不相等实根为
.集合
，
{2，4，5，6}，
{1，2，3，4}，A∩C＝A，A∩B＝
，求
的值.
；
.相关知识点
推荐套卷
（本小题满分14分）已知四棱锥P—ABCD的三视图如右图所示，
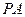其中正（主）视图与侧（左）视为直角三角形，俯视图为正方形。 （1）求四棱锥P—ABCD的体积； （2）若E是侧棱上的动点。问：不论点E在PA的
任何位置上，是否都有？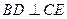
请证明你的结论？
（3）求二面角D—PA—B的余弦值。
粤公网安备 44130202000953号