分)已知:如图,矩形ABCD,PA⊥平面ABCD, M、N、R分别是AB、PC、CD的中点.
(1)求证:直线MN⊥直线AB ;


 (2)若PA=AB=2,AD=1,求直线NR与平面PAR所成角的大小;
(2)若PA=AB=2,AD=1,求直线NR与平面PAR所成角的大小;
(3)若平面PDC与平面ABCD所成的二面角为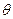 ,能否确定
,能否确定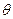 使直线MN是异面直线AB与PC的公垂线,若能确定,求出
使直线MN是异面直线AB与PC的公垂线,若能确定,求出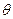 的值,若不能确定,说明理由.
的值,若不能确定,说明理由.


 |
推荐套卷
分)已知:如图,矩形ABCD,PA⊥平面ABCD, M、N、R分别是AB、PC、CD的中点.
(1)求证:直线MN⊥直线AB ;


 (2)若PA=AB=2,AD=1,求直线NR与平面PAR所成角的大小;
(2)若PA=AB=2,AD=1,求直线NR与平面PAR所成角的大小;
(3)若平面PDC与平面ABCD所成的二面角为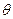 ,能否确定
,能否确定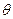 使直线MN是异面直线AB与PC的公垂线,若能确定,求出
使直线MN是异面直线AB与PC的公垂线,若能确定,求出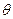 的值,若不能确定,说明理由.
的值,若不能确定,说明理由.


 |