（本小题满分15分）
如图，某单位用木料制作如图所示的框架,框架的下部是边长分别为
(单位:米)的矩形,上部是斜边长为
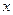的等腰直角三角形，要求框架围成的总面积为8平方米.
（Ⅰ）求的关系式，并求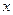的取值范围；
（Ⅱ）问分别为多少时用料最省?
.推荐套卷
（本小题满分15分）
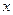如图，某单位用木料制作如图所示的框架,框架的下部是边长分别为(单位:米)的矩形,上部是斜边长为的等腰直角三角形，要求框架围成的总面积为8平方米.
（Ⅰ）求的关系式，并求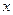的取值范围；
（Ⅱ）问分别为多少时用料最省?
粤公网安备 44130202000953号