在长方体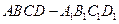 中,
中, 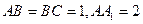 ,
,
点 是
是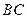 的中点,点
的中点,点 是
是 的中点.
的中点.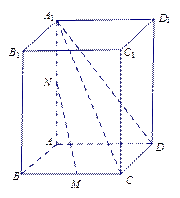
(Ⅰ)求证: 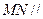 平面
平面 ;
;
(Ⅱ)求异面直线 和
和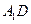 所成的角余弦值;
所成的角余弦值;
(Ⅲ)过 三点的平面把长方体
三点的平面把长方体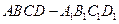 截成
截成
两部分几何体, 求所截成的两部分几何体的体积的比值.
推荐套卷
在长方体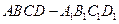 中,
中, 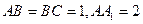 ,
,
点 是
是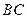 的中点,点
的中点,点 是
是 的中点.
的中点.
(Ⅰ)求证: 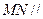 平面
平面 ;
;
(Ⅱ)求异面直线 和
和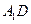 所成的角余弦值;
所成的角余弦值;
(Ⅲ)过 三点的平面把长方体
三点的平面把长方体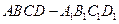 截成
截成
两部分几何体, 求所截成的两部分几何体的体积的比值.