如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧面PAD是正三角形且与底面ABCD垂直
，E是AB的中点，PC与平面ABCD所成角为
．
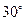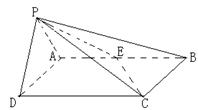
（1）求二面角P-CE-D的大小；
（2）当AD为多长时，点D到平面PCE 的距离为2．
相关试题
中，底面
为菱形，其中
，
，
为
的中点．
； 
平面
为
的中点，求四棱锥
的体积．
，曲线
上点
处的切线方程为
.
时有极值，求
上的最值及相应的
的值.
．
的最小正周期；
时，求函数
．
中，曲线
的参数方程为
（
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为：
（其中
为常数）．
时，求曲线推荐套卷
如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧面PAD是正三角形且与底面ABCD垂直，E是AB的中点，PC与平面ABCD所成角为．
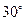（1）求二面角P-CE-D的大小；
（2）当AD为多长时，点D到平面PCE 的距离为2．
粤公网安备 44130202000953号