已知a，b∈R，函数f(x)＝a＋ln(x＋1)的图象与g(x)＝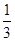
x3－
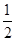x2＋bx的图象在交点(0,0)处有公共切线．
(1)证明：不等式f(x)≤g(x)对一切x∈(－1，＋∞)恒成立；
(2)设－1＜x1＜x2，当x∈(x1，x2)时，证明：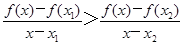
.
相关试题
交圆
于
两点，
是直径，
平分
，交圆
， 过
丄
.
,求
的面积
，曲线
在点
处的切线方程为
的值
的三条不同切线，求
的取值范围
处的切线都过点（0,2），证明：当
时，
的两个极值点为
，求
的取值范围。
的最小值
，试讨论此函数的单调性。推荐套卷
已知a，b∈R，函数f(x)＝a＋ln(x＋1)的图象与g(x)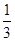＝x3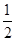－x2＋bx的图象在交点(0,0)处有公共切线．
(1)证明：不等式f(x)≤g(x)对一切x∈(－1，＋∞)恒成立；
(2)设－1＜x1＜x2，当x∈(x1，x2)时，证明：.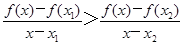
粤公网安备 44130202000953号