如图,在矩形 中,
中, ,以
,以 为圆心1为半径的圆与
为圆心1为半径的圆与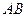 交于
交于 (圆弧
(圆弧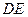 为圆在矩形内的部分)
为圆在矩形内的部分)
(1)在圆弧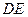 上确定
上确定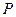 点的位置,使过
点的位置,使过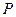 的切线
的切线 平分矩形ABCD的面积;
平分矩形ABCD的面积;
(2)若动圆 与满足题(1)的切线
与满足题(1)的切线 及边
及边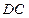 都相切,试确定
都相切,试确定 的位置,使圆
的位置,使圆 为矩形内部面积最大的圆.
为矩形内部面积最大的圆.
推荐套卷
如图,在矩形 中,
中, ,以
,以 为圆心1为半径的圆与
为圆心1为半径的圆与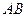 交于
交于 (圆弧
(圆弧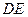 为圆在矩形内的部分)
为圆在矩形内的部分)
(1)在圆弧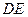 上确定
上确定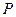 点的位置,使过
点的位置,使过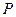 的切线
的切线 平分矩形ABCD的面积;
平分矩形ABCD的面积;
(2)若动圆 与满足题(1)的切线
与满足题(1)的切线 及边
及边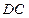 都相切,试确定
都相切,试确定 的位置,使圆
的位置,使圆 为矩形内部面积最大的圆.
为矩形内部面积最大的圆.