(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 |
7 |
8 |
9 |
10 |
| 命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为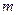 次、
次、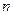 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“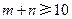 ”的概率.
”的概率.
推荐套卷
(本题满分1 3分)
3分)
某运动员进行20次射击练习,记录了他射击的有关数据,得到下表:
| 环数 |
7 |
8 |
9 |
10 |
| 命中次数 |
2 |
7 |
8 |
3 |
(Ⅰ)求此运动员射击的环数的平均数;
(Ⅱ)若将表中某一环数所对应的命中次数作为一个结果,在四个结果(2次、7次、8次、3次)中,随机取2个不同的结果作为基本事件进行研究,记这两个结果分别为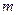 次、
次、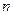 次,每个基本事件为(m,n).
次,每个基本事件为(m,n).
求“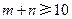 ”的概率.
”的概率.